7.4 Junção de tabelas utilizando funções4

O pacote base do R fornece uma função que executa essa ação, chamada merge(). Porém, há alguns tipos de junções não podem ser executados com esta função, o que nos levará ao uso de vetores lógicos em conjunto com a função interaction(). Daremos exemplos com essas duas novas maneiras.

7.4.1 Dados para nossa prática

Utilizaremos três tabelas para esta prática:

  1. O data.frame tab1 possui nomes de famílias, gêneros e epítetos específicos de algumas angiospermas:
familia <- c("Burseraceae", "Solanaceae", "Sapindaceae", "Rubiaceae", "Lauraceae")
generos <- c("Protium", "Trattinnickia", "Dacryodes", "Duckeodendron", "Markea", "Solanum", "Allophylastrum", "Cupania", "Thinouia", "Psychotria", "Duroia", "Cinchona", "Ocotea", "Licaria", "Rhodostemonodaphne", "Anisophyllea", "Freziera")
epitetos <- c("aracouchini", "burserifolia", "edilsonii", "cestroides", "ulei", "cyathophorum", "frutescens", "rubiginosa", "myriantha", "viridis", "eriopila", "amazonica", "delicata", "aureosericea", "recurva", "manausensis", "carinata")
tab1 <- data.frame(familia = c(rep(familia, each = 3), "Anisophylleaceae", "Pentaphylacaceae"), genero = generos, epiteto = epitetos, stringsAsFactors = FALSE)
Tabela 7.1: Tabela 1
familia genero epiteto
Burseraceae Protium aracouchini
Burseraceae Trattinnickia burserifolia
Burseraceae Dacryodes edilsonii
Solanaceae Duckeodendron cestroides
Solanaceae Markea ulei
Solanaceae Solanum cyathophorum
Sapindaceae Allophylastrum frutescens
Sapindaceae Cupania rubiginosa
Sapindaceae Thinouia myriantha
Rubiaceae Psychotria viridis
Rubiaceae Duroia eriopila
Rubiaceae Cinchona amazonica
Lauraceae Ocotea delicata
Lauraceae Licaria aureosericea
Lauraceae Rhodostemonodaphne recurva
Anisophylleaceae Anisophyllea manausensis
Pentaphylacaceae Freziera carinata
  1. O data.frame tab2 contem um conjunto pequeno com alguns nomes de famílias, gêneros, e o nome de seus respectivos clados acima dos nomes de ordens segundo o APG (2016):
familia2 <- c("Burseraceae", "Solanaceae", "Sapindaceae", "Rubiaceae", "Annonaceae")
generos2 <- c("Protium", "Duckeodendron", "Thinouia", "Psychotria", "Guatteria")
clado <- c("Malvids", "Lamiids", "Malvids", "Lamiids", "Magnoliids")
tab2 <- data.frame(familia = familia2, genero = generos2, clado = clado, stringsAsFactors = FALSE)
Tabela 7.2: Tabela 2
familia genero clado
Burseraceae Protium Malvids
Solanaceae Duckeodendron Lamiids
Sapindaceae Thinouia Malvids
Rubiaceae Psychotria Lamiids
Annonaceae Guatteria Magnoliids
  1. O data.frame tab3 corresponde à tabela 2, tab2, sem as famílias Solanaceae e Rubiaceae:
tab3 <- subset(tab1, familia %in% c("Burseraceae", "Sapindaceae"))
Tabela 7.3: Tabela 3
familia genero epiteto
1 Burseraceae Protium aracouchini
2 Burseraceae Trattinnickia burserifolia
3 Burseraceae Dacryodes edilsonii
7 Sapindaceae Allophylastrum frutescens
8 Sapindaceae Cupania rubiginosa
9 Sapindaceae Thinouia myriantha

7.4.2 Maneira 3 - função merge()

O básico para entender a função merge() é saber que existem dois argumentos, x e y, que correspondem aos data.frames de entrada. Quando unimos tabelas, existem junções que adicionam variáveis, e junções que filtram variáveis. Vamos ver abaixo 4 tipos da primeira ( junção interna, junção à esquerda, junção à direita, junção total), e dois tipos desta última ( semijunção e antijunção).

7.4.2.1 Junção interna

Ao juntarmos tabelas x e y, temos todas as linhas de x em que há valores em comum com y, e todas as colunas de x e y. Se houver múltiplas correspondências entre x e y, todas as combinações retornam.

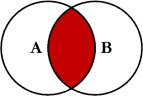
Fonte: www.sqlfromhell.com

Em nosso exemplo, vamos unir as tabelas 1 e 2. Ambas possuem em comum os identificadores familia e genero. Para facilitar o entendimento, vamos verificar primeiro cada tabela com cores para checar as correspondências entre x e y nas variáveis em comum:

Tabela 7.4: Tabela 1
familia genero epiteto
Burseraceae Protium aracouchini
Burseraceae Trattinnickia burserifolia
Burseraceae Dacryodes edilsonii
Solanaceae Duckeodendron cestroides
Solanaceae Markea ulei
Solanaceae Solanum cyathophorum
Sapindaceae Allophylastrum frutescens
Sapindaceae Cupania rubiginosa
Sapindaceae Thinouia myriantha
Rubiaceae Psychotria viridis
Rubiaceae Duroia eriopila
Rubiaceae Cinchona amazonica
Lauraceae Ocotea delicata
Lauraceae Licaria aureosericea
Lauraceae Rhodostemonodaphne recurva
Anisophylleaceae Anisophyllea manausensis
Pentaphylacaceae Freziera carinata
Tabela 7.5: Tabela 2
familia genero clado
Burseraceae Protium Malvids
Solanaceae Duckeodendron Lamiids
Sapindaceae Thinouia Malvids
Rubiaceae Psychotria Lamiids
Annonaceae Guatteria Magnoliids

Reparem que os valores em que há correspondência entre x e y estão coloridos de amarelo; para os em que não há correspondência, estão coloridos de vermelho. Agora, executemos a junção das duas tabelas:

merge(x = tab1, y = tab2)
familia genero epiteto clado
Burseraceae Protium aracouchini Malvids
Rubiaceae Psychotria viridis Lamiids
Sapindaceae Thinouia myriantha Malvids
Solanaceae Duckeodendron cestroides Lamiids

Vejam que houve a incorporação dos valores da coluna epiteto, presente apenas na tabela 2, em que há correspondência entre as tabelas 1 e 2. É importante notar que as famílias Lauraceae, Anisophylleaceae, e Pentaphylacaceae ficaram de fora, pois não são encontradas na tabela y, isto é, a tabela 2, assim como seus respectivos gêneros e epítetos associados a estes. Gêneros presentes na tabela 1 de famílias em comum entre ambas as tabelas também não foram incorporados nessa junção, pois nãp encontram correspondência na tabela 2: Dacryodes, Trattinnickia, Markea, Solanum, Allophylastrum, Cupania, Duroia, Cinchona. Revejam o conceito de junção interna para entender o porquê desse acontecimento.

7.4.2.2 Junção à esquerda

Ao juntarmos tabelas x e y, temos todas as linhas de x, e todas as colunas de x e y. Linhas em x sem correspência em y terão valores NA adicionados nas novas colunas. Se houver múltiplas correspondências entre x e y, todas as combinações retornam.

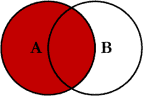
Fonte: www.sqlfromhell.com

Continuaremos utilizando as tabelas 1 e 2. Como mostrado anteriormente, ambas possuem em comum os identificadores familia e genero. Chequemos novamente as cores das correspondências dentro de cada identificador, coloridas em amarelo:

Tabela 7.6: Tabela 1
familia genero epiteto
Burseraceae Protium aracouchini
Burseraceae Trattinnickia burserifolia
Burseraceae Dacryodes edilsonii
Solanaceae Duckeodendron cestroides
Solanaceae Markea ulei
Solanaceae Solanum cyathophorum
Sapindaceae Allophylastrum frutescens
Sapindaceae Cupania rubiginosa
Sapindaceae Thinouia myriantha
Rubiaceae Psychotria viridis
Rubiaceae Duroia eriopila
Rubiaceae Cinchona amazonica
Lauraceae Ocotea delicata
Lauraceae Licaria aureosericea
Lauraceae Rhodostemonodaphne recurva
Anisophylleaceae Anisophyllea manausensis
Pentaphylacaceae Freziera carinata
Tabela 7.7: Tabela 2
familia genero clado
Burseraceae Protium Malvids
Solanaceae Duckeodendron Lamiids
Sapindaceae Thinouia Malvids
Rubiaceae Psychotria Lamiids
Annonaceae Guatteria Magnoliids

Em uma junção à esquerda, todas as linhas de x retornam após a junção. Para executar este tipo de junção, acrescentaremos um novo argumento, all.x = TRUE, indicando que manteremos todas as linhas de x, isto é, o data.frame à esquerda, que é a tabela 1.

merge(x = tab1, y = tab2, all.x = TRUE)
familia genero epiteto clado
Anisophylleaceae Anisophyllea manausensis NA
Burseraceae Dacryodes edilsonii NA
Burseraceae Protium aracouchini Malvids
Burseraceae Trattinnickia burserifolia NA
Lauraceae Licaria aureosericea NA
Lauraceae Ocotea delicata NA
Lauraceae Rhodostemonodaphne recurva NA
Pentaphylacaceae Freziera carinata NA
Rubiaceae Cinchona amazonica NA
Rubiaceae Duroia eriopila NA
Rubiaceae Psychotria viridis Lamiids
Sapindaceae Allophylastrum frutescens NA
Sapindaceae Cupania rubiginosa NA
Sapindaceae Thinouia myriantha Malvids
Solanaceae Duckeodendron cestroides Lamiids
Solanaceae Markea ulei NA
Solanaceae Solanum cyathophorum NA

Agora, temos uma nova situação. Para os valores de x sem correspondência em y, valores NA são acrescentados. Reparem na coluna clado e vejam que isso ocorreu apenas nesta variável. Por exemplo, vejam a família Anisophylleaceae. Ela ocorre apenas na tabela 1 e, portanto, não possui nenhum valor de cladoa ssociado a ela, pois esta variável ocorre apenas na tabela 2. Com a junção das tabelas, essa variável é retida, porém sem a existência de um valor para a família, é inserido então o valor NA. Temos também o caso de Annonaceae, presente na tabela 2. A família não é recuperada na junção interna, pois ela não existe na tabela 1 dentro da variável familia e, portanto, não apresenta correspondência com nenhum dado da tabela 1. Revejam o conceito de junção à esquerda para entender o porquê desse acontecimento.

7.4.2.3 Junção à direita

Ao juntarmos tabelas x e y, temos todas as linhas de y, e todas as colunas de x e y.Linhas em y sem correspência em x terão valores NA adicionados nas novas colunas. Se houver múltiplas correspondências entre x e y, todas as combinações retornam.

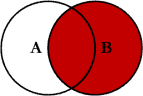
Fonte: www.sqlfromhell.com

De maneira oposta à junção à esquerda, na junção à direita são mantidas todas as linhas de y. Desta vez, o argumento a ser utilizado é all.y = TRUE. Antes de executar a junção, vamos checar novamente as variáveis em comum e correspondências entre as tabelas x e y:

Tabela 7.8: Tabela 1
familia genero epiteto
Burseraceae Protium aracouchini
Burseraceae Trattinnickia burserifolia
Burseraceae Dacryodes edilsonii
Solanaceae Duckeodendron cestroides
Solanaceae Markea ulei
Solanaceae Solanum cyathophorum
Sapindaceae Allophylastrum frutescens
Sapindaceae Cupania rubiginosa
Sapindaceae Thinouia myriantha
Rubiaceae Psychotria viridis
Rubiaceae Duroia eriopila
Rubiaceae Cinchona amazonica
Lauraceae Ocotea delicata
Lauraceae Licaria aureosericea
Lauraceae Rhodostemonodaphne recurva
Anisophylleaceae Anisophyllea manausensis
Pentaphylacaceae Freziera carinata
Tabela 7.9: Tabela 2
familia genero clado
Burseraceae Protium Malvids
Solanaceae Duckeodendron Lamiids
Sapindaceae Thinouia Malvids
Rubiaceae Psychotria Lamiids
Annonaceae Guatteria Magnoliids

Agora executaremos a junção com o comando abaixo. Não deixem de reparar no uso do argumento all.y = TRUE, pois ele é o responsável por agora manter todas as linhas da tabela 2 (== y):

merge(x = tab1, y = tab2, all.y = TRUE)
familia genero epiteto clado
Annonaceae Guatteria NA Magnoliids
Burseraceae Protium aracouchini Malvids
Rubiaceae Psychotria viridis Lamiids
Sapindaceae Thinouia myriantha Malvids
Solanaceae Duckeodendron cestroides Lamiids

Notem que agora todos os dados da tabela 2 foram mantidos. Houve a inserção de um valor NA para a família Annonaceae na variável epiteto, pois esta variável não está presente na tabela 2. Revejam o conceito de junção à direita para entender o porquê desse acontecimento.

7.4.2.4 Junção total

Ao juntarmos tabelas x e y, temos todas as linhas e colunas de x e y. Onde não houver valores correspondentes, valores NA serão colocados nesses lugares.

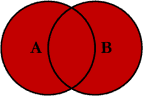
Fonte: www.sqlfromhell.com

Em uma junção total, uniremos todas as linha de x e y utilizando o argumento all = TRUE.

merge(x = tab1, y = tab2, all = TRUE)
familia genero epiteto clado
Anisophylleaceae Anisophyllea manausensis NA
Annonaceae Guatteria NA Magnoliids
Burseraceae Dacryodes edilsonii NA
Burseraceae Protium aracouchini Malvids
Burseraceae Trattinnickia burserifolia NA
Lauraceae Licaria aureosericea NA
Lauraceae Ocotea delicata NA
Lauraceae Rhodostemonodaphne recurva NA
Pentaphylacaceae Freziera carinata NA
Rubiaceae Cinchona amazonica NA
Rubiaceae Duroia eriopila NA
Rubiaceae Psychotria viridis Lamiids
Sapindaceae Allophylastrum frutescens NA
Sapindaceae Cupania rubiginosa NA
Sapindaceae Thinouia myriantha Malvids
Solanaceae Duckeodendron cestroides Lamiids
Solanaceae Markea ulei NA
Solanaceae Solanum cyathophorum NA

Reparem que valores NA são colocados nos valores da tabela 2 referentes à coluna epiteto, ausente na tabela 1. O mesmo se passa com valores da coluna clado, presente na tabela 2 e ausente na tabela 1. Revejam o conceito de junção total para entender o porquê desse acontecimento.

7.4.2.5 Semijunção

Ao juntarmos tabelas x e y, temos todas as linhas de x onde houver valores correspondentes em y, mantendo apenas colunas de x. É parecida com a junção interna, porém difere desta por nunca duplicar valores de x, retornando sempre apenas valores de x que houver uma correspondência em y.

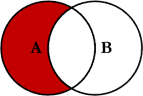
Fonte: www.sqlfromhell.com

A semijunção é muito similar à junção interna, diferindo desta por não incorporar as colunas de y, pois apenas utiliza esta tabela para filtrar os dados de x, constituindo-se então em um tipo de junção que filtra variáveis. Neste exemplo, utilizaremos as tabelas 1 e 3. Ambas compartilham as colunas familia e genero. Vamos checar primeiramente cada tabela e ver o que é compartilhado entre cada uma:

Tabela 7.10: Tabela 1
familia genero epiteto
Burseraceae Protium aracouchini
Burseraceae Trattinnickia burserifolia
Burseraceae Dacryodes edilsonii
Solanaceae Duckeodendron cestroides
Solanaceae Markea ulei
Solanaceae Solanum cyathophorum
Sapindaceae Allophylastrum frutescens
Sapindaceae Cupania rubiginosa
Sapindaceae Thinouia myriantha
Rubiaceae Psychotria viridis
Rubiaceae Duroia eriopila
Rubiaceae Cinchona amazonica
Lauraceae Ocotea delicata
Lauraceae Licaria aureosericea
Lauraceae Rhodostemonodaphne recurva
Anisophylleaceae Anisophyllea manausensis
Pentaphylacaceae Freziera carinata
Tabela 7.11: Tabela 3
familia genero epiteto
1 Burseraceae Protium aracouchini
2 Burseraceae Trattinnickia burserifolia
3 Burseraceae Dacryodes edilsonii
7 Sapindaceae Allophylastrum frutescens
8 Sapindaceae Cupania rubiginosa
9 Sapindaceae Thinouia myriantha
7.4.2.5.1 Maneira 4 - vetores lógicos e a função interaction()

Para executar uma semijunção com o pacote base do R, devemos fazer uso de vetores lógicos e da função interaction(), pois a função merge() não fornece uma maneira de se obter o que desejamos.

Vamos então à prática5. As colunas compartilhadas por ambas as tabelas serão nossas chaves:

chaves <- c("familia", "genero")

Partimos então para filtrar na tabela 1 a combinação de linhas para esse conjunto de colunas utilizando a função interaction() do pacote base do R:

interaction(tab1[, chaves])
##  [1] Burseraceae.Protium           Burseraceae.Trattinnickia    
##  [3] Burseraceae.Dacryodes         Solanaceae.Duckeodendron     
##  [5] Solanaceae.Markea             Solanaceae.Solanum           
##  [7] Sapindaceae.Allophylastrum    Sapindaceae.Cupania          
##  [9] Sapindaceae.Thinouia          Rubiaceae.Psychotria         
## [11] Rubiaceae.Duroia              Rubiaceae.Cinchona           
## [13] Lauraceae.Ocotea              Lauraceae.Licaria            
## [15] Lauraceae.Rhodostemonodaphne  Anisophylleaceae.Anisophyllea
## [17] Pentaphylacaceae.Freziera    
## 119 Levels: Anisophylleaceae.Allophylastrum ... Solanaceae.Trattinnickia

Essa função computa um vetor de fatores que representa a interação das colunas fornecidas na tabela 1. Se fizermos isso com a tabela 3, poderemos saber quais combinações ocorrem em ambas as tabelas.

interaction(tab3[, chaves])
## [1] Burseraceae.Protium        Burseraceae.Trattinnickia 
## [3] Burseraceae.Dacryodes      Sapindaceae.Allophylastrum
## [5] Sapindaceae.Cupania        Sapindaceae.Thinouia      
## 12 Levels: Burseraceae.Allophylastrum ... Sapindaceae.Trattinnickia

Agora utilizamos a mesma função interaction e o operador %in% para retornar um vetor lógico que utilizaremos para filtrar os valores da tabela 1 com correspondência na tabela 3.

linhas <- interaction(tab1[, chaves]) %in% interaction(tab3[, chaves])
linhas
##  [1]  TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE FALSE
tab1[linhas, ]
familia genero epiteto
1 Burseraceae Protium aracouchini
2 Burseraceae Trattinnickia burserifolia
3 Burseraceae Dacryodes edilsonii
7 Sapindaceae Allophylastrum frutescens
8 Sapindaceae Cupania rubiginosa
9 Sapindaceae Thinouia myriantha

7.4.2.6 Antijunção

Retorna todas as linhas de x em que não há correspondência em y, mantendo apenas colunas de x.

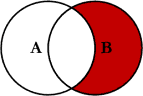
Fonte: www.sqlfromhell.com

Uma antijunção é ligeiramente diferente de uma semijunção pois ela retorna todas as linhas de x que não aparecem em y. Portanto, podemos utilizar o inverso de nosso vetor lógico linhas e utilizar este inverso para filtrar as linhas da tabela 1 e ter nossa tabela antijunção entre x e y:

antilinhas <- !linhas
tab1[antilinhas, ]
familia genero epiteto
4 Solanaceae Duckeodendron cestroides
5 Solanaceae Markea ulei
6 Solanaceae Solanum cyathophorum
10 Rubiaceae Psychotria viridis
11 Rubiaceae Duroia eriopila
12 Rubiaceae Cinchona amazonica
13 Lauraceae Ocotea delicata
14 Lauraceae Licaria aureosericea
15 Lauraceae Rhodostemonodaphne recurva
16 Anisophylleaceae Anisophyllea manausensis
17 Pentaphylacaceae Freziera carinata

Referências

APG. 2016. "An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG IV". Botanical Journal of the Linnean Society 181: 1--20.

  1. Texto publicado originalmente no blog de R.O.Perdiz (https://www.ricardoperdiz.com/blog/2020-04-juncao-tbl/)↩︎

  2. Esta solução de semijunção é baseada no tutorial do pacote poorman, recém-criado para emular as funções do pacote dplyr.↩︎